令人惊叹的对称数学

数学家华罗庚（1910-1985）说过，“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的……认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美。下面这一组美图，将带你走进一个极致的数学美学世界！

露叶毛毡苔科

Hoya Aldrichii

你一定已经发现，它们之所以看起来如此赏心悦目，除了晶莹润泽的色彩外，还因为它们有着完美的几何图形!有些具有分形，有些则具有对称性。

多叶芦荟，又称螺旋芦荟

多叶芦荟的叶子紧密地按逆时针(或顺时针)方向螺旋，通常有五层螺旋，每层都排列成一个均匀的圆形，和植株整体形状相同。

非洲菊

自然界中这些神奇的几何图案除了给人以美的感受，也给人以智慧的启迪。你想到了什么？

半边莲

卷心菜剖面

伽利略就曾说：“自然界伟大的书是用数学语言写成的，其特征为三角形、圆形和其他几何图形，没有这些几何图形，人们只能在黑暗的迷宫中做毫无结果的游荡”。

向日葵

菱叶丁香蓼

造物主用几何的语言在这些缤纷繁复的图案中藏下自然的美与智慧，祂是数学家中的数学家！

多肉

某种蕨类的叶子梯就像梯子一样排列着。

欣赏了以上大自然为我们打开的美图，你在思考什么？

这个充满着规律的世界，其实时时刻刻，无处不在向人们诉说着关于数学的故事！

人类的智慧也是无穷无尽的，它把大自然中蕴含的数学知识一一挖掘出来并加以运用，下面再来看一组数学应用于建筑的精彩案例。

一、黄金分割

埃及金字塔

金字塔在埃及和美洲等地均有分布，古埃及的上埃及、中埃及和下埃及，今苏丹和埃及境内。现在的尼罗河下游，散布着约80座金字塔遗迹。大小不一，其中最高大的是胡夫金字塔，高146.5米，底长230米，共用230万块平均每块2.5吨的石块砌成，占地52000平方公尺。

石块之间没有任何黏着物，靠石块的相互叠压和咬合垒成。国王哈佛拉的金字塔前，还矗立着一座象征国王权力与尊严的狮身人面像。埃及金字塔是古埃及的帝王（法老）陵墓。世界七大奇迹之一。数量众多，分布广泛。开罗西南尼罗河西古城孟菲斯一带的金字塔是占有集中的一部分。

金字塔底面边长与高之比约为11：7，恰好为祖冲之发现的约率22/7=3.142857的一半。

巴特农神庙

巴特农神庙之名出于雅典娜的别号。其立面高与宽的比例为19:31，接近希腊人喜爱的“黄金分割比 ”，因此具有独特的美感。

东方明珠

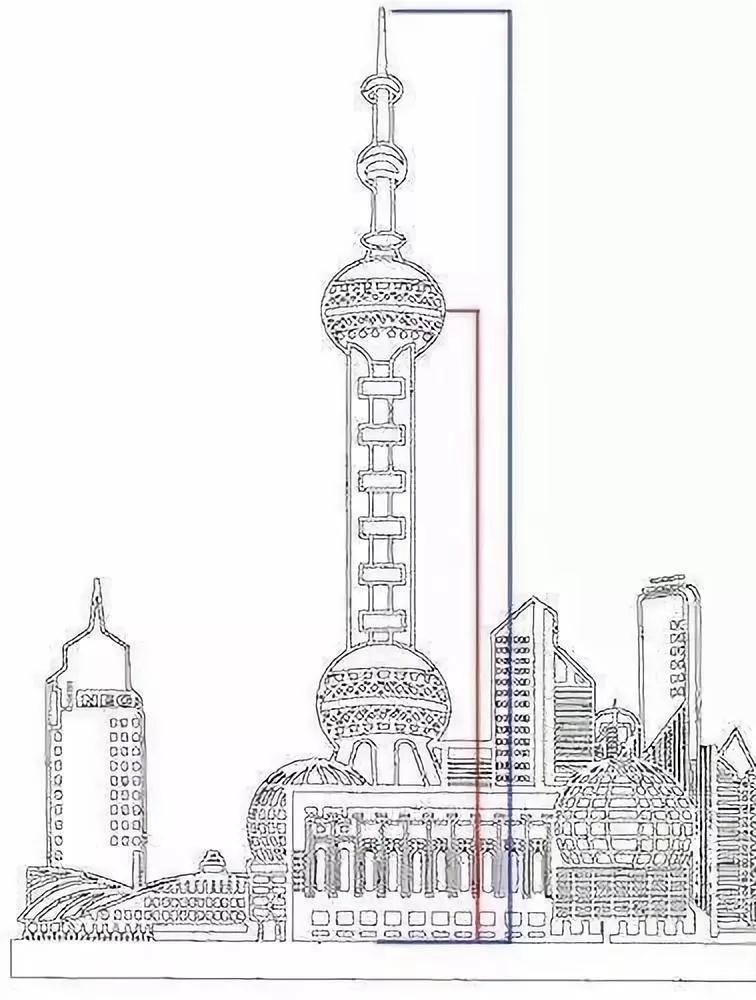
上海东方明珠电视塔的塔高468m，上球体到塔底的距离约为289.2m，二者之比非常接近黄金比例0.618，因此显得格外挺拔。

二、膜结构

“水立方”是北京奥运会国家游泳中心，它的膜结构是世界之最。它是根据细胞排列形式和肥皂泡天然结构设计而成的，这种形态在建筑结构中从来没有出现过，创意十分奇特。

水立方

而肥皂泡中蕴含了丰富的数学问题，比如什么样的泡沫结构效率最高？这个问题叫做开尔文问题，至今仍是未解之谜。

阳光谷

位于上海世博园的阳光谷是中国第一的索膜结构建筑，其特殊之处在于柔性，白色膜布的最大风摆幅可以达到上下3米，大风吹来，膜布能随风起舞。而这种膜结构和微分几何中的极小曲面关系密切。

三、单叶双曲面&双曲抛物面

广州塔

俗称“小蛮腰”的广州塔采取的是单叶双曲面的结构。由于单叶双曲面是一种双重直纹曲面，它可以用直的钢梁建造。这样会减少风的阻力，同时，也可以用最少的材料来维持结构的完整。除了广州塔以外，许多发电厂和冷却塔也是这种结构。
圣玛丽教堂

位于旧金山的圣玛丽教堂采取的是双曲抛物面的结构，也叫做“马鞍面”。马鞍面是罗氏几何的一个重要模型。另外，我们常吃的某些薯片就是马鞍面哦。

四、球形结构&拱形结构

富勒球

富勒设计的蒙特利尔世博会美国馆，被人亲切地称为“富勒球”。这样的设计在现代已随处可见。然而这种不需要柱、梁、拱顶等支撑物的建筑模式在当时遭到很多人的怀疑。三位化学家从中，深受启发，发现了的新碳球C60的晶体形态，并最终获得了1996年诺贝尔化学奖。

悉尼歌剧院的形状实际上参照了同一个被拨开的球体的扇形部分，也就是说，这些曲面可以同属一个球面方程。它解决了开展大规模制造、加工零件的精度问题以及简单装配问题。

悉尼歌剧院

另外，球形或椭球形结构的好处在于坚固——比如生鸡蛋是很难用手握碎的。这是因为球形的任何一个地方受力，力都可以向四周均匀地分散开来。巨大的贮油罐做成球形就是这个道理。电灯泡为了更透光，玻璃壳很薄，但做成球形，它就比较坚固了。此外，安全帽盔，锅盖，雨伞等物品的设计里也有类似的原理。

赵州桥

球形是若干个拱形的组合，因此拱形也具有坚固的特点。这也是为什么大部分的桥要设计成拱形的原因了，比如我国著名的赵州桥。因为这种形状更坚固，可以使受力分散，进而桥体的承重力加大。

五、对称结构

泰姬陵

在所有的建筑中，最对称的建筑之一就是印度的泰姬陵。不仅主体建筑对称，就连水池边的瓷砖花纹、树木都对称。不仅左右对称，由于在水的倒映下，还上下对称。这种对称的构成能表达秩序、安静与稳定、庄重与威严等心理感觉，并能给人以美感。

故宫博物院

故宫博物院采取严格的中轴对称的布局方式：中轴线上的建筑高大华丽，轴线两侧的建筑相对低小简单，同样给人一种庄严肃穆的感觉。

六、悬链线

金门大桥

位于美国旧金山的金门大桥，是世界著名的桥梁之一，被国际桥梁工程界广泛认为是美的典范。金门大桥是一种悬索桥，用到了数学上悬链线的原理，而悬链线方程的发现在数学史上还是一段趣闻呢。

圣路易斯拱门

圣路易斯拱门，就是美国向西开发的一个象征，这座雄伟壮观的不锈钢悬链线的建筑物，高达192米，是1964年动工后仅用两年时间建成的。拱门底部有电梯可以直达顶层。圣路易斯拱门为圣路易斯市的地标， 高630英尺， 比华盛顿纪念碑、自由女神像或是欧洲的比萨斜塔都还要高！

据说根据设计要求，拱门顶端的正常摆动幅度可在46公分之内，但据科学家计算，“大拱门”即使遇到时速80公里的大风，其摆动幅度也仅有5公分。

七、莫比乌斯带

凤凰卫视北京总部大楼

包裹在格子的玻璃和钢皮，这个由建筑工作室BIAD的环形建筑为中国广播电视凤凰卫视提供了新的总部。

两个具有肾形平面图的球根塔被玻璃和钢皮包围，以创建建筑物的环形形状。

卷的倾斜轮廓表示一个塔比另一个塔高几层。建筑师将设计与Mbius带的扭曲形式相比较。

建筑师说：“这两个部分很难实现和谐的效果，但是在这个方案中，我们采用了将高层办公楼与媒体广播厅相结合的莫比斯模式。“独特的建筑形状结合了朝阳公园的自然景观。”

凤凰卫视北京总部大楼的设计灵感就来自有名的“莫比乌斯带”。把一根纸条扭转180°后，两头再粘接起来即可做成其模型。莫比乌斯带是一种不可定向的曲面，一只小虫可以爬遍整个曲面而不必跨过它的边缘。

长沙中国结步行桥

湖南长沙的中国结步行桥位于梅溪湖上，该步行桥于2014年6月开工，全长183.95米，相对高度20.425米，由直线形“散步道”和拱形“登山道”多段桥身交叉组成。

其设计灵感源于中国传统工艺形式——中国结，同时加入了西方数学家发现的莫比乌斯环的结构特征，寓意梅溪湖地区不断突破发展，被评为“世界最性感建筑”。笔者在大学期间去上面走过，当时还正在修建中。

曲面细分&极小曲面

现代的一些建筑师喜欢做曲面的建筑，为了降低成本，通常的做法往往是化曲为直，用种类有限而数量巨大的多边形来拼合出外表皮。这是蕴含着极其复杂的算法的，通常是各大曲面设计所的核心机密，算法好坏的一个评判标准是表皮的流畅程度。

广州大剧院

广州大剧院宛如两块被珠江水冲刷过的灵石，奇特的外形充满奇思妙想。全球顶级声学大师为广州大剧院精心打造的声学系统，达到世界一流水平，使其传递出近乎完美的视听效果，获得全球建筑界及艺术家的极高评价，为中国夺得无数殊荣。

慕尼黑奥运会场馆

在数学中，极小曲面是指平均曲率为零的曲面。举例来说，满足某些约束条件的面积最小的曲面。物理学中，由最小化面积而得到的极小曲面的实例可以是沾了肥皂液后吹出的肥皂泡。肥皂泡的极薄的表面薄膜称为皂液膜，这是满足周边空气条件和肥皂泡吹制器形状的表面积最小的表面。

赞赏

微信赞赏支付宝赞赏